집합(set)
집합(set)은 원소(element)라고 불리는 서로 다른 객체들의 모임으로 현대 수학에서 가장 기초가 되는 개념이다.
집합은 정확하게 정의되어야 하며, 어떤 객체가 그 집합에 속하는지 아닌지를 분명히 구분할 수 있어야 한다.
집합을 표현하는 방법은 두가지가 있다.
- 원소나열법 : 집합의 원소들을 { } 사이에 하나씩 나열하는 방법.
ex) S = { 1, 2, 3, 4, 5 } - 조건제시법 : 집합의 원소들이 가지고 있는 특정한 성질을 기술하여 나타내는 방법.
표현은 S = {x | p(x)}와 같이 나타낸다.
여기서 x는 원소를 대변하는 변수이고, p(x)는 원소들이 가지고 있는 성질을 나타낸다.
ex) 2부터 4까지의 자연수의 집합 : S = { x | x는 자연수이고 1 < x < 5 }
카디날리티(Cardinality)
집합 S 내에 있는 서로 다른 원소들의 개수를 그 집합의 카디날리티(cardinality) 또는 원소 수라고 하고
|S|로 표기한다.
ex) 집합 A = {1, 3, 5, 7, 9}의 원소는 5개, 집합 B = {1}의 원소는 1개, 집합 N = {1, 2, 3, .... }의 원소는 무한이므로
|A| = 5, |B| = 1, |N| = ∞
유한 집합(finite set) / 무한 집합(infinite set)
집합 S의 원소의 개수가 유한인 경우, 집합 S를 유한집합(finite set)이라 하며,집합 S가 유한 집합이 아니면, 집합 S를 무한 집합(infinite set)이라고 한다.
ex) 지금 이 시각 모든 지구 사람들의 집합 = 유한집합
6의 배수인 자연수의 집합 = 무한집합
집합 S1에서 집합 S2로의 일대일 대응인 함수가 존재할 때,
S1과 S2가 같은 카디날리티를 가지고 있다고 한다.
ex)
S1 = { 0, 1, 2 }
S2 = { a, b, c }
= 두 집합 모두 카디날리티가 3으로 같다.
전체집합의 표기와 기호의 국제적 공인 기호들
Z : 정수의 집합 // Z = { ... , -2, -1, 0, 1, 2, ... }
N : 자연수의 집합 // N = { x | x ∈ Z, x > 0} = {1, 2, 3, ... }
R : 실수의 집합
Q : 유리수의 집합 // Q = { x/y | x, y ∈ Z, y가 0이 아닐 때 }
Sn : 1부터 n까지의 자연수의 집합 // Sn = { x | x ∈ N, x <= n}
밴 다이어그램
주어진 집합의 원소들은 모두 전체 집합 U의 원소가 되므로, 모든 집합은 전체 집합 U의 부분집합이라고 할 수 있다.
즉, 집합의 연산에서 만들어지는 새로운 집합들은 주어진 집합의 원소들을 조합함으로써 만들어진다.
주어진 집합들 사이의 관계와 집합의 연산에 대하여 이해하기 쉽도록 밴 다이어그램을 활용한다.
전체 집합 U는 사각형으로 나타내고 주어진 집합들은 U의 부분집합들이므로, 사각형 안에 원으로 표현한다.
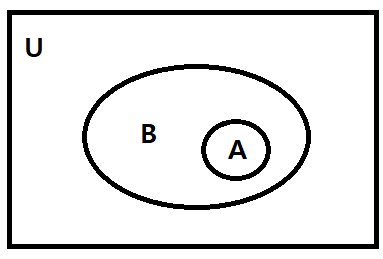
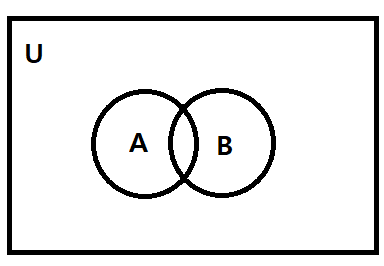
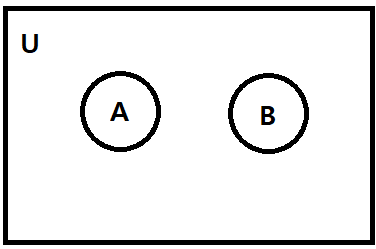
집합의 연산
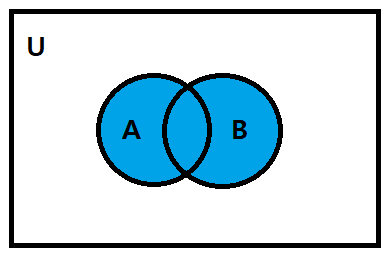
합집합 (Union) : A∪B
임의의 두 집합 A, B에 대하여 이들의 합집합은 집합 A 또는 집합 B에 속하는 모든 원소의 집합을 말하며
A∪B로 표기한다.
A∪B = { x | x ∈ A ∨ x ∈ B }
// 원소 x는 A에 속하며 또는(OR) B에 속한다.
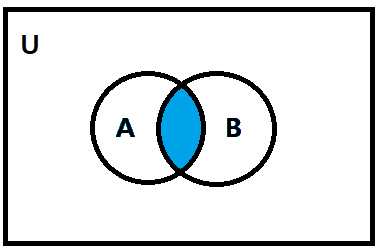
교집합(Intersection) : A∩B
임의의 두 집합 A, B에 대하여 이들의 교집합은 집합 A에도 속하고 집합 B에도 속하는 모든 원소의 집합을 말하며,
A∩B로 표기한다.
A∩B = { x | x ∈ A ∧ x ∈ B }
// 원소 x는 A에 속한다. 그리고(AND) 원소 x는 B에도 속한다.
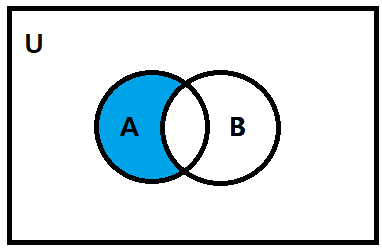
차집합(Difference) : A - B
임의의 두 집합 A, B에 대하여 이들의 차집합은 집합 A에 속하고 집합 B에는 속하지 않는 모든 원소들의 집합을 말하며,
A - B로 표기한다.
A - B = { x | x ∈ A ∧ x !∈ B}
// 원소 x는 A에 속한다. 그리고 B에는 속하지 않는다.
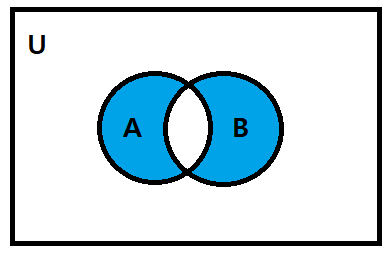
대칭 차집합(Symmetric difference) : A⊕B
임의의 두 집합 A, B에 대하여 이들의 대칭 차집합은 A∪B의 원소 중에서 A∩B에 속하지 않는 모든 원소들의 집합을 말하며, A⊕B로 표시한다.
A⊕B = { x | x ∈ A U B ∧ x !∈ A ∩ B }
= { x | x ∈ A - B ∨ x ∈ B - A }
= { x | (x ∈ A ∧ x !∈ B) ∨ (x !∈ A ∧ x ∈ B)}
// x가 A와 B의 합집합에 속하면서 A와 B의 교집합은 아니다.
// x가 A와 B의 차집합에 속하거나 x가 B와 A의 차집합에 속한다.
// x가 A에 속하면서 B에는 속하지 않거나 또는 x가 A에 속하지 않으면서 B에는 속한다.
곱집합(Cartisian production) : A X B
임의의 두 집합 A, B의 곱집합 또는 카티시안 곱(Cartisian production)은 x ∈ A이고
y ∈ B인 모든 순서쌍 (x, y)의 집합을 말하며 A X B로 표기한다.
예를들어 A = { 1, 2, 3 }, B = { a, b, c } 일 때
A x B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c), (3, a), (3, b), (3, c)}