유클리드 알고리즘
- 유클리드 알고리즘은 두 자연수의 최대공약수를 효과적으로 구하는 알고리즘이다.
- 두 자연수의 최대공약수를 알고 있다면, 두 자연수의 최소공배수도 쉽게 구할 수 있다.
두 자연수의 최대공약수를 구하는 원시적인 방법은 아래와 같다.
- 각각 자연수의 약수들을 전개한다.
- 전개된 약수 들 중 공통된 숫자들을 곱한다.

하지만 각 자연수의 약수를 구하는 작업은 굉장히 번거롭다.
프로그래밍적으로도 시간이 많이 걸리는 작업이다.
이를 간단히 해결하기 위해 두 자연수의 최대공약수를 구할때는 유클리드 알고리즘을 사용한다.
유클리드 알고리즘은 유클리드 호제법이라고도 한다.
https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
유클리드 호제법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 유클리드 호제법(-互除法, Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이다. 호제법이란
ko.wikipedia.org
이 게시글은 유클리드 알고리즘의 증명을 다루고 있지는 않다.
알고리즘에 대한 증명이 궁금하다면 위의 위키백과 또는 인터넷에서 유클리드 알고리즘 증명을 검색해서
찾아보자!
구현

a = 78696, b = 19332의 최대공약수를 구해보자.
원시적인 방법을 사용하면 상당한 시간이 걸릴 것인데, 유클리드 알고리즘을 사용하면
몇번의 나눗셈만으로도 최대공약수를 구할 수 있다.
최초
a = 78696, b = 19332
a % b = 1368
a = 19332
b = 1368
두번째
a = 19332, b = 1368
a % b = 180
a = 1368
b = 180
세번째
a = 1368, b = 180
a % b = 108
a = 180
b = 108
네번째
a = 180
a % b = 72
a = 108
b = 72
다섯번쨰
a = 108
a % b = 36
a = 72
b = 36
여섯번째 (끝)
a = 72
a % b = 0
a = 36 (최대공약수)
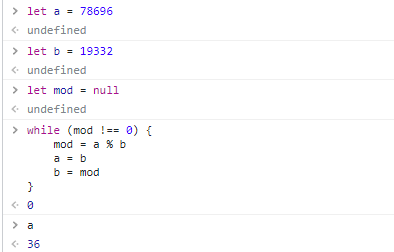
이를 자바스크립트 코드로 옮기면 아래와 같다.
let a = 78696
let b = 19332
let mod = null
while (mod !== 0) {
mod = a % b
a = b
b = mod
}
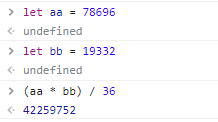
최대공약수로 최소공배수 구하기
최소공배수 = a x b / 최대공약수
'알고리즘, 자료구조' 카테고리의 다른 글
| [자료구조-JS] 이진탐색트리(Binary Search Tree) 구현 (0) | 2023.06.01 |
|---|---|
| [정수론] 에라토스테네스의 체 / 배열 구현 (0) | 2023.05.22 |
| [자료구조-JS] 더블 링크드 리스트 구현 (0) | 2023.03.13 |
| [자료구조-JS] 싱글 링크드 리스트 구현 (0) | 2023.03.05 |
| [정렬] 퀵정렬 (0) | 2022.11.27 |
