에라토스테네스의 체
- 고대 그리스 수학자인 에라토스테네스가 고안했다.
- 주어진 자연수보다 작거나 같은 소수들이 어떤 것들이 있는지 찾아내는 알고리즘이다.
- 주어진 자연수 만큼 표를 그려놓은 뒤, 소수의 배수들을 지워나간다. 최종적으로 남은 숫자들은 소수이다.
자연수 25에 소수가 몇개 포함되어 있는지 에라토스테네스의 체를 이용해 판별해보자.
| 1 | 2 | 3 | 5 | |
| 7 | ||||
| 11 | 13 | |||
| 17 | 19 | |||
| 23 |
- 자연수 1은 소수가 아니다.
- 2는 유일한 짝수인 소수이다. 2는 소수로써 남겨두고 2의 배수들은 전부 지워준다.
- 3은 소수이다. 3은 소수로써 남겨두고 3의 배수들은 전부 지워준다.
- 4는 이미 합성수라고 이전에 결론이 났다. 넘어간다.
- 5는 소수이다. 5는 소수로써 남겨두고 5의 배수들은 전부 지워준다.
- 6은 합성수니까 넘어간다.
- 7은 소수이다. 7은 소수로써 남겨두고 7의 배수들은 전부 지워준다. ...
이러한 과정을 거치면 자연수 25의 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23 임을 알 수 있다.
프로그래밍으로 이를 구현해보자.
배열 구현
- 아이디어 : 배열의 인덱스를 자연수로 보고, 엘리먼트값을 소수와 합성수로 본다.
- 값이 true면 소수, false면 합성수이다.
- 자연수 N개 만큼의 배열을 만든다. (배열은 0부터 시작이고, 소수는 2부터 시작이니 이를 고려해야 한다.)
- 0과 1을 제외한 배열의 엘리먼트를 모두 true로 채운다.
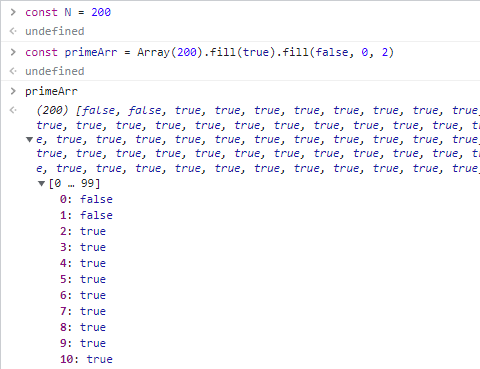
- 2부터 소수이므로, 반복문의 초기 시작은 2부터 시작한다. 반복문의 종료조건은 N의 제곱근으로 한다.
- 제곱근으로 하는 이유는 아래에서 따로 기술하겠다.
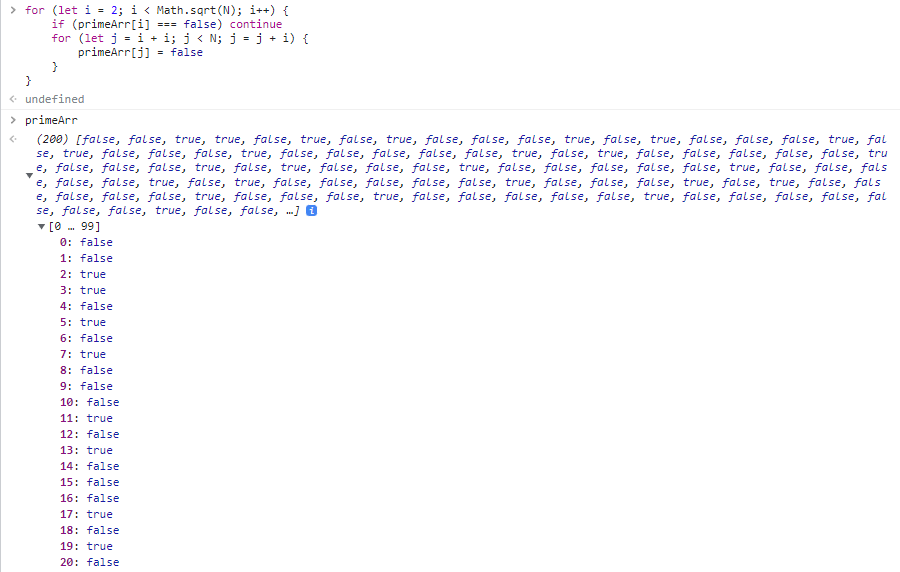
- 소수의 배수를 지워나가야 하므로 primeArr[i]이 합성수라면 continue를 통해 다음 반복문으로 이동한다.
- primeArr[i]이 소수라면 루프가 진행되며 i의 배수들이 모두 false가 된다.
에라토스테네스 체 코드
const N = 200
const primeArr = Array(200).fill(true).fill(false, 0, 2)
for (let i = 2; i < Math.sqrt(N); i++) {
if (primeArr[i] === false) continue
for (let j = i + i; j < N; j = j + i) {
primeArr[j] = false
}
}
외부 반복문의 종료조건을 i < Math.sqrt(N)으로 하는 이유
i를 N만큼 돌려도 문제는 해결된다. 하지만 효율적이지 않기에 Math.sqrt(N)으로 진행한다.
별도의 증명과정을 통해 제곱근으로 하는 것이 더 효율적이라는 것을 알 수 있다.
n 이하의 모든 소수들을 구한다고 가정해보자.
n은 자연수 a, b에 대해 n = a * b 라고 할 수 있을 것이다.
그리고 m = Math.sqrt(N) 에 대해 n = m * m 이라고도 할 수 있을 것이다.
즉 a * b = m * m 이어야 한다.
이 때 a와 b가 자연수가 되려면
a = m, a = m 또는
a < m, b > m 또는
a > m, b < m이 되어야 할 것이다.
즉 a와 b가 m과 같지 않다면 a와 b 둘 중 작은 값 하나는 m보다는 작을 것이다. (5 * 11이나 11 * 5나 같다.)
그러므로 i의 범주를 Math.sqrt(N)까지만 잡아도 전체 체의 합성수를 찾아낼 수 있다.
'알고리즘, 자료구조' 카테고리의 다른 글
| [자료구조-JS] 이진탐색트리 너비우선탐색(BFS) 구현 (0) | 2023.06.02 |
|---|---|
| [자료구조-JS] 이진탐색트리(Binary Search Tree) 구현 (0) | 2023.06.01 |
| [정수론] 유클리드 알고리즘 / 최대공약수, 최소공배수 (0) | 2023.05.22 |
| [자료구조-JS] 더블 링크드 리스트 구현 (0) | 2023.03.13 |
| [자료구조-JS] 싱글 링크드 리스트 구현 (0) | 2023.03.05 |
에라토스테네스의 체
- 고대 그리스 수학자인 에라토스테네스가 고안했다.
- 주어진 자연수보다 작거나 같은 소수들이 어떤 것들이 있는지 찾아내는 알고리즘이다.
- 주어진 자연수 만큼 표를 그려놓은 뒤, 소수의 배수들을 지워나간다. 최종적으로 남은 숫자들은 소수이다.
자연수 25에 소수가 몇개 포함되어 있는지 에라토스테네스의 체를 이용해 판별해보자.
| 1 | 2 | 3 | 5 | |
| 7 | ||||
| 11 | 13 | |||
| 17 | 19 | |||
| 23 |
- 자연수 1은 소수가 아니다.
- 2는 유일한 짝수인 소수이다. 2는 소수로써 남겨두고 2의 배수들은 전부 지워준다.
- 3은 소수이다. 3은 소수로써 남겨두고 3의 배수들은 전부 지워준다.
- 4는 이미 합성수라고 이전에 결론이 났다. 넘어간다.
- 5는 소수이다. 5는 소수로써 남겨두고 5의 배수들은 전부 지워준다.
- 6은 합성수니까 넘어간다.
- 7은 소수이다. 7은 소수로써 남겨두고 7의 배수들은 전부 지워준다. ...
이러한 과정을 거치면 자연수 25의 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23 임을 알 수 있다.
프로그래밍으로 이를 구현해보자.
배열 구현
- 아이디어 : 배열의 인덱스를 자연수로 보고, 엘리먼트값을 소수와 합성수로 본다.
- 값이 true면 소수, false면 합성수이다.
- 자연수 N개 만큼의 배열을 만든다. (배열은 0부터 시작이고, 소수는 2부터 시작이니 이를 고려해야 한다.)
- 0과 1을 제외한 배열의 엘리먼트를 모두 true로 채운다.

- 2부터 소수이므로, 반복문의 초기 시작은 2부터 시작한다. 반복문의 종료조건은 N의 제곱근으로 한다.
- 제곱근으로 하는 이유는 아래에서 따로 기술하겠다.

- 소수의 배수를 지워나가야 하므로 primeArr[i]이 합성수라면 continue를 통해 다음 반복문으로 이동한다.
- primeArr[i]이 소수라면 루프가 진행되며 i의 배수들이 모두 false가 된다.
에라토스테네스 체 코드
const N = 200
const primeArr = Array(200).fill(true).fill(false, 0, 2)
for (let i = 2; i < Math.sqrt(N); i++) {
if (primeArr[i] === false) continue
for (let j = i + i; j < N; j = j + i) {
primeArr[j] = false
}
}
외부 반복문의 종료조건을 i < Math.sqrt(N)으로 하는 이유
i를 N만큼 돌려도 문제는 해결된다. 하지만 효율적이지 않기에 Math.sqrt(N)으로 진행한다.
별도의 증명과정을 통해 제곱근으로 하는 것이 더 효율적이라는 것을 알 수 있다.
n 이하의 모든 소수들을 구한다고 가정해보자.
n은 자연수 a, b에 대해 n = a * b 라고 할 수 있을 것이다.
그리고 m = Math.sqrt(N) 에 대해 n = m * m 이라고도 할 수 있을 것이다.
즉 a * b = m * m 이어야 한다.
이 때 a와 b가 자연수가 되려면
a = m, a = m 또는
a < m, b > m 또는
a > m, b < m이 되어야 할 것이다.
즉 a와 b가 m과 같지 않다면 a와 b 둘 중 작은 값 하나는 m보다는 작을 것이다. (5 * 11이나 11 * 5나 같다.)
그러므로 i의 범주를 Math.sqrt(N)까지만 잡아도 전체 체의 합성수를 찾아낼 수 있다.
'알고리즘, 자료구조' 카테고리의 다른 글
| [자료구조-JS] 이진탐색트리 너비우선탐색(BFS) 구현 (0) | 2023.06.02 |
|---|---|
| [자료구조-JS] 이진탐색트리(Binary Search Tree) 구현 (0) | 2023.06.01 |
| [정수론] 유클리드 알고리즘 / 최대공약수, 최소공배수 (0) | 2023.05.22 |
| [자료구조-JS] 더블 링크드 리스트 구현 (0) | 2023.03.13 |
| [자료구조-JS] 싱글 링크드 리스트 구현 (0) | 2023.03.05 |
