집합 사이의 관계를 표현하는 방법은 몇 가지가 있다.
집합 A = {1, 2, 3}에서 원소 a, b가 a > b인 관계 R 과 같이 표현하는 서술식 방법도 있고
그 서술식에 따라 관계를 순서쌍들의 집합으로 {(1, b) ... ~ } 나열하는 나열식 방법도 있다.
그 외에도 순서쌍의 원소들 간의 관계를 편리하게 표현하기 위한 방법으로
화살표 도표(arrow diagram), 좌표 도표(coordinate diagram),
방향 그래프(directed graph), 관계 행렬(relation matrix) 등이 있다.
화살표 도표(arrow diagram)
관계 a가 집합 A의 원소이고 b가 집합 B의 원소라고 하면 (a, b) ∈ R 일 경우
집합 A에 있는 원소 a에서 집합 B에 있는 원소 b로 화살표를 그려서 관계를 표현한다.
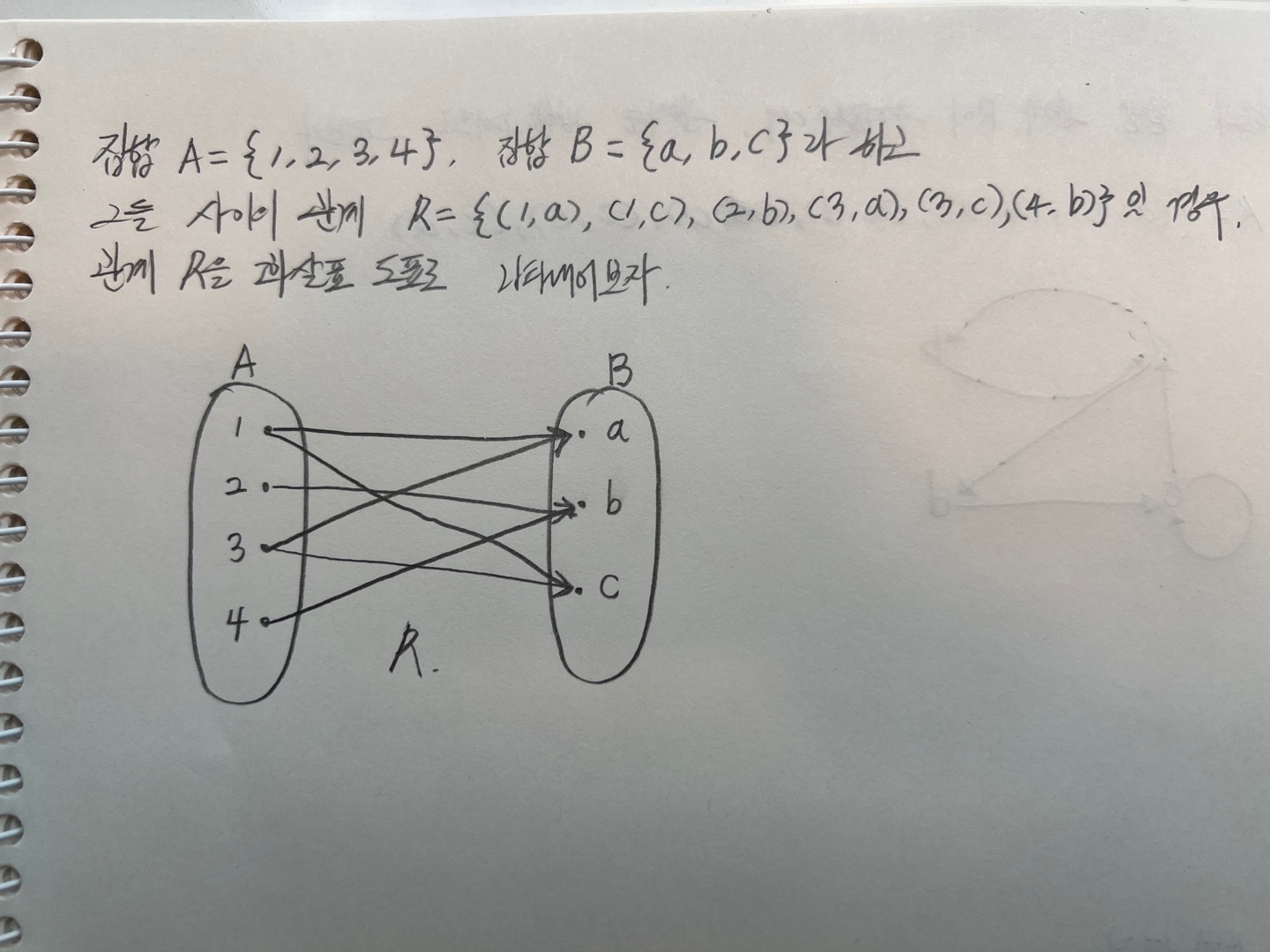
좌표 도표(coordinate diagram)
집합 A의 원소를 x축 위의 점으로 표시하고 집합 B의 원소를 y축 위의 점으로 생각하여
a ∈ A와 b ∈ B의 관계가 있으면 a를 가리키는 x 좌표축과 b를 가리키는 y 좌표축이 만나는 곳에 점으로 표시한다.
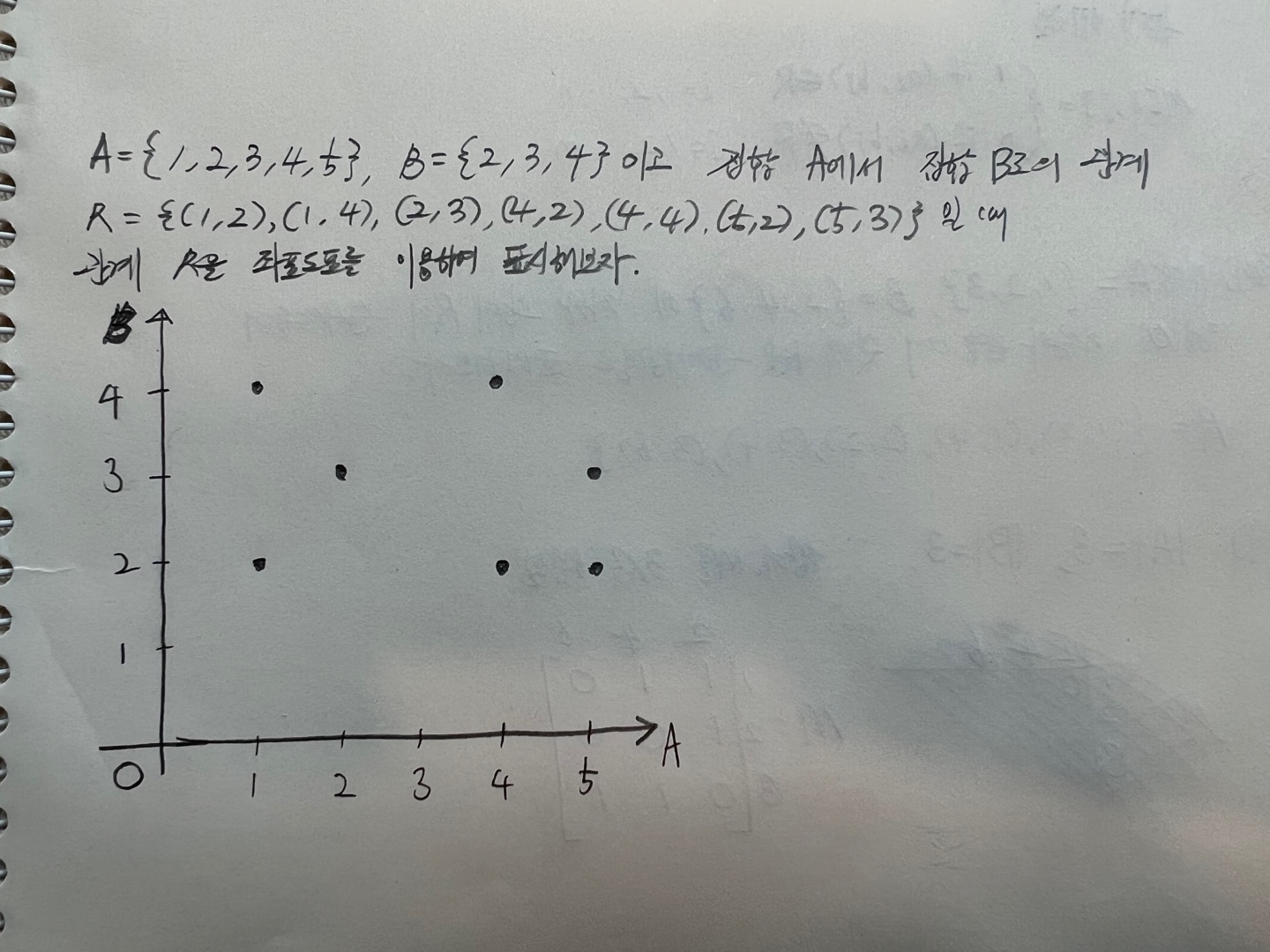
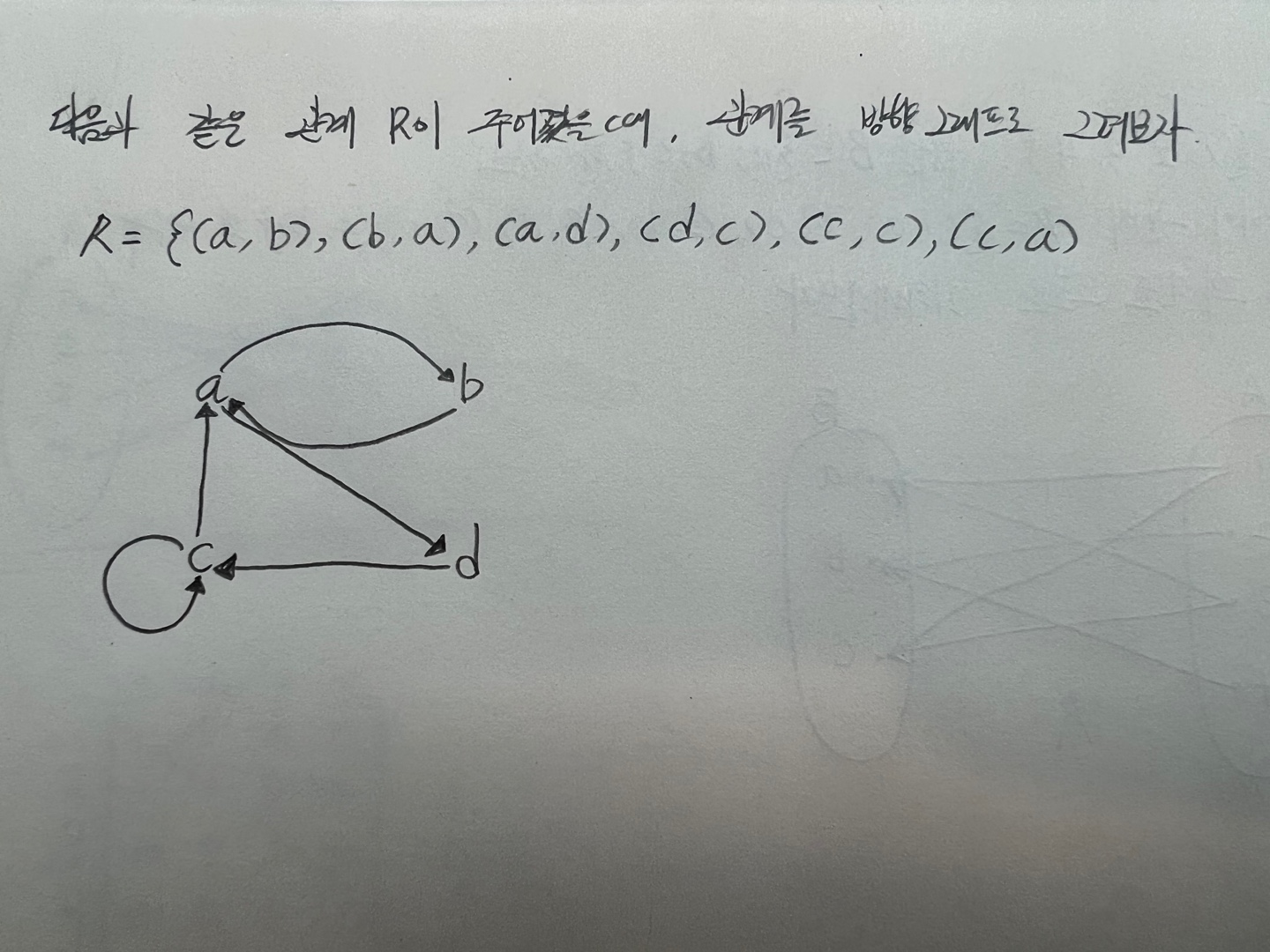
방향 그래프(directed graph)
관계 R이 두 집합 A와 B 사이의 관계가 아니고
하나의 집합 A에 대한 관계일 때, 각 집합 A의 각 원소를 그래프의 정점(vertex)으로 표시하고
(a, b) ∈ R일 경우 a에서 b로의 화살표가 있는 연결선(edge)으로 표현하는 것을
관계 R에 대한 방향 그래프라고 한다.
관계 행렬(Relation Matrix)
관계를 부울 행렬(Boolean Matrix, Zero-One Matrix)을 통해 표현하는 방법이다.
부울 행렬은 행렬 안에 있는 모든 원소들이 0 또는 1로 표시되는 행렬을 의미한다.
즉 관계 행렬의 행에는 집합 A의 원소, 열에는 집합 B의 원소를 표시하는데,
행렬의 각 요소의 값은 a ∈ A와 b ∈ B의 관계가 있으면 1, 그렇지 않으면 0으로 표현하는 방법이다.

'했던것들 > 이산수학' 카테고리의 다른 글
| 관계 (Relation) (0) | 2022.05.26 |
|---|---|
| 프로그램의 입증 (0) | 2022.05.25 |
| 여러가지 증명법 (0) | 2022.05.25 |
| 연역법(deduction)과 귀납법(induction) (0) | 2022.05.25 |
| 집합(set) (0) | 2022.05.24 |
집합 사이의 관계를 표현하는 방법은 몇 가지가 있다.
집합 A = {1, 2, 3}에서 원소 a, b가 a > b인 관계 R 과 같이 표현하는 서술식 방법도 있고
그 서술식에 따라 관계를 순서쌍들의 집합으로 {(1, b) ... ~ } 나열하는 나열식 방법도 있다.
그 외에도 순서쌍의 원소들 간의 관계를 편리하게 표현하기 위한 방법으로
화살표 도표(arrow diagram), 좌표 도표(coordinate diagram),
방향 그래프(directed graph), 관계 행렬(relation matrix) 등이 있다.
화살표 도표(arrow diagram)
관계 a가 집합 A의 원소이고 b가 집합 B의 원소라고 하면 (a, b) ∈ R 일 경우
집합 A에 있는 원소 a에서 집합 B에 있는 원소 b로 화살표를 그려서 관계를 표현한다.

좌표 도표(coordinate diagram)
집합 A의 원소를 x축 위의 점으로 표시하고 집합 B의 원소를 y축 위의 점으로 생각하여
a ∈ A와 b ∈ B의 관계가 있으면 a를 가리키는 x 좌표축과 b를 가리키는 y 좌표축이 만나는 곳에 점으로 표시한다.

방향 그래프(directed graph)
관계 R이 두 집합 A와 B 사이의 관계가 아니고
하나의 집합 A에 대한 관계일 때, 각 집합 A의 각 원소를 그래프의 정점(vertex)으로 표시하고
(a, b) ∈ R일 경우 a에서 b로의 화살표가 있는 연결선(edge)으로 표현하는 것을
관계 R에 대한 방향 그래프라고 한다.

관계 행렬(Relation Matrix)
관계를 부울 행렬(Boolean Matrix, Zero-One Matrix)을 통해 표현하는 방법이다.
부울 행렬은 행렬 안에 있는 모든 원소들이 0 또는 1로 표시되는 행렬을 의미한다.
즉 관계 행렬의 행에는 집합 A의 원소, 열에는 집합 B의 원소를 표시하는데,
행렬의 각 요소의 값은 a ∈ A와 b ∈ B의 관계가 있으면 1, 그렇지 않으면 0으로 표현하는 방법이다.

'했던것들 > 이산수학' 카테고리의 다른 글
| 관계 (Relation) (0) | 2022.05.26 |
|---|---|
| 프로그램의 입증 (0) | 2022.05.25 |
| 여러가지 증명법 (0) | 2022.05.25 |
| 연역법(deduction)과 귀납법(induction) (0) | 2022.05.25 |
| 집합(set) (0) | 2022.05.24 |
